Dr Stephen Millmore (12 hours)
Lectures:
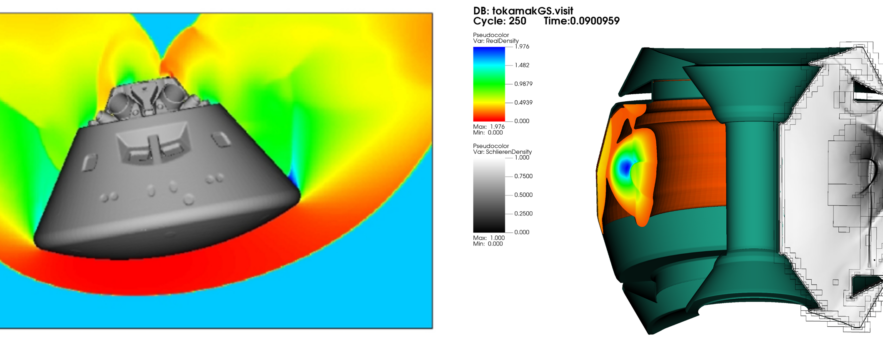
- Mesh generation for continuum modelling (Part 1) (Dr N. Gokhale)
Overview of grid generation techniques; comparison of different mesh types; introduction to cut cell methods; meshing from STL files - Mesh generation for continuum modelling (Part 2) (Dr N. Gokhale)
Geometric information in cut cell methods; the small cell problem and cut cell approaches; the flux stabilisation cut cell method; convergence properties of cut cell methods - Source terms and equations of state (Part 1)
Including body forces and other source terms in hyperbolic systems of equations; simple coordinate transformations; derivation of the ideal gas equation of state; mathematical quantities for an equation of state - Equations of state (Part 2) and magnetohydrodynamics (Part 1)
Equations of state for gases, liquids and solids; reference quantities for defining material properties; tabulated equations of state; modelling a plasma; combining Maxwell’s equations with the Euler equations - Magnetohydrodynamics (Part 2)
Mathematical properties of the magnetohydrodynamics equations (MHD); numerical methods for MHD; the divergence constraint; from ideal to resistive MHD; MHD for simulating lightning - Elastoplastic solids
Compressible models for simulating solids; stress, strain and strength; high strain-rate behaviour; evolution equations for an elastoplastic solid; separating elastic and plastic effects
Practicals:
- Two-dimensional Euler equations (Part 1)
Modification of one-dimensional schemes to work in two dimensions, with application to multi-dimensional problems - Two-dimensional Euler equations (Part 2)
Continuation of the first practical - Geometric source terms
Allowing one-dimensional codes to run for cylindrical and spherical symmetry, and two-dimensional codes to run in cylindrical symmetry, comparing to results from previous practicals - Beyond the ideal equation of state
Simulating problems with the stiffened gas equation of state for shocked water, and a Mie-Grüneisen equation of state for a high-speed solid - Magnetohydrodynamics (Part 1)
Developing a code to solve for one-dimensional MHD problems, with the simulation of multi-wave shock tube tests - Magnetohydrodynamics (Part 2)
Continuation of the previous practical